Publication Date: June 28, 2024
Authors: Danial Motlagh and Nathan Wiebe
Abstract:
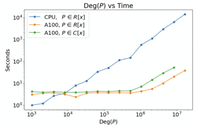
Quantum signal processing (QSP) and quantum singular value transformation (QSVT) currently stand as the most efficient techniques for implementing functions of block-encoded matrices, a central task that lies at the heart of most prominent quantum algorithms. However, current QSP approaches face several challenges, such as the restrictions imposed on the family of achievable polynomials and the difficulty of calculating the required phase angles for specific transformations. In this paper, we present a generalized quantum signal processing (GQSP) approach, employing general SU(2) rotations as our signal-processing operators, rather than relying solely on rotations in a single basis. Our approach lifts all practical restrictions on the family of achievable transformations, with the sole remaining condition being that |𝑃|≤1, a restriction necessary due to the unitary nature of quantum computation. Furthermore, GQSP provides a straightforward recursive formula for determining the rotation angles needed to construct the polynomials in cases where 𝑃 and 𝑄 are known. In cases where only 𝑃 is known, we provide an efficient optimization algorithm capable of identifying in under a minute of GPU time, a corresponding 𝑄 for polynomials of degree on the order of 107. We further illustrate GQSP simplifies QSP-based strategies for Hamiltonian simulation, offer an optimal solution to the 𝜖-approximate fractional query problem that requires 𝒪((1/𝛿)+log (1/𝜖)) queries to perform where 𝒪(1/𝛿) is a proved lower bound, and introduces novel approaches for implementing bosonic operators. Moreover, we propose a novel framework for the implementation of normal matrices, demonstrating its applicability through synthesis of diagonal matrices, as well as the development of a new algorithm for convolution through synthesis of circulant matrices using only 𝒪(𝑑log 𝑁+log2 𝑁) 1 and 2-qubit gates for a filter of lengths 𝑑.