Publication Date: February 14, 2025
Authors:
Noah Lupu-Gladstein, Ou Teen Arthur Pang, Hugo Ferretti, Weng-Kian Tham, Aephraim M. Steinberg, Kent Bonsma-Fisher, and Aharon Brodutch
Abstract:
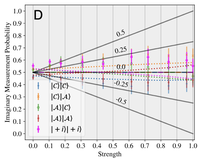
We implement a variant of the quantum pigeonhole paradox thought experiment to study whether classical counting principles survive in the quantum domain. We observe strong measurements significantly violate the pigeonhole principle (that among three pigeons in two holes, at least one pair must be in the same hole) and the sum rule (that the number of pigeon pairs in the same hole is the sum of the number of pairs across each of the holes) in an ensemble that is pre- and postselected into particular separable states. To investigate whether measurement disturbance is a viable explanation for these counterintuitive phenomena, we employ a we employ variable-strength nonlocal measurements. As we decrease the measurement strength, we find the violation of the sum rule decreases, yet the pigeonhole principle remains violated. In the weak limit, the sum rule is restored due to the cancellation between two weak values with equal and opposite imaginary parts. We observe the same kind of cancellation at higher measurement strengths, thus raising the question: do strong measurements have imaginary parts?
Related links:
Read this publication on the PNAS website