Publication Date: 23 October, 2024
Authors: YuZheng Xie, Andrew Hardy, and Arun Paramekanti
Abstract:
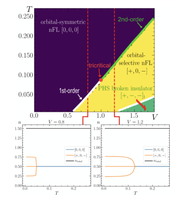
Motivated by systems where a high-temperature non-Fermi liquid gives way to low-temperature ℤ3 Potts nematic order, we studied a three-orbital Sachdev-Ye-Kitaev (SYK) model in the large-𝑁 limit. In the single-site limit, this model exhibits a spontaneous orbital selective transition which preserves average particle-hole symmetry, with two orbitals becoming insulators while the third orbital remains a non-Fermi liquid down to zero temperature. We extend this study to lattice models of three-orbital SYK dots, exploring uniform symmetry-broken states on the triangular and cubic lattices. At high temperature, these lattice models exhibit an isotropic non-Fermi-liquid metal phase. On the three-dimensional cubic lattice, the low-temperature uniform ℤ3 nematic state corresponds to an orbital selective layered state which preserves particle-hole symmetry at small hopping and spontaneously breaks the particle-hole symmetry at large hopping. Over a wide range of temperatures, the transport in this layered state shows metallic in-plane resistivity but insulating out-of-plane resistivity. On the two-dimensional triangular lattice, the low-temperature state with uniform orbital order is also a correlated ℤ3 nematic with orbital selective transport but it remains metallic in both principal directions. We discuss a Landau theory with ℤ3 clock terms which captures salient features of the phase diagram and nematic order in all these models. We also present results on the approximate wave-vector-dependent orbital susceptibility of the isotropic non-Fermi-liquid states.
Related links: